Petri Nets Log #003

siiky

2022/07/23

2022/07/24

en

Language

Following up with the idea of a Petri nets programming language, I now have some goals I want it to meet:

• It has to be a real programming language, not a modeling one!
• Must be textual, human-friendly, and text-editor-friendly -- I don't want to have to muck with a shitty, slow, and subpar GUI editor (as a bonus: this should be enough to make it VCS-friendly too)
• In line with the first point: transitions are written in the "host" programming language, and the user must be able to reuse existing code of that language
• Also in line with the first point: a program in this language must be runnable (even better if compiled) like any other program
• It must be easy to convert to a graphical representation of places, transitions, and edges between them
• It would be fucking great if transitions and nets were reusable and composable! This is possibly one of the hardest goals, so as a start I'm OK with supporting only monolithic nets

Here's a starting point: places can be identified, or referenced, in a Petri net by integers:

(define-constant p0 0)
(define-constant p1 1)
(define-constant p2 2)
(define-constant p3 3)

There's a DSL that makes it easy to define transitions. Transitions have the associated input and output places, and a transition procedure. This procedure is user code in the host language, and is how the net model ties with "normal" code.

; Consumes two tokens from p0: x and y
(define-transition (t1 (x p0) (y p0))
  (p1 p2)
  ; Produces (+ x y) to p1, and #t to p2
  (values (+ x y) #t))

; Consumes res from p1 and succ? from p2
(define-transition (t2 (res p1) (succ? p2))
  (p3)
  ; The value of this expression isn't used because p3 is a "terminal" place
  (when succ? (print "Successfully sumed: " a)))

Finally, a Petri net is simply the set of its transitions:

(define-petri-net some-net t1 t2)

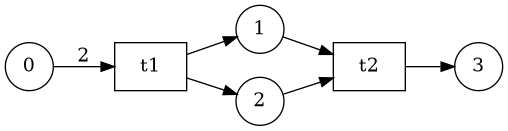
With two different macro implementations of define-transition and define-petri-net it's easy to have the same source file expand to compilable code and to some graphical representation (such as GVS, which can be converted to GraphViz, which can be converted to PNG, SVG, &c, with a couple of commands).

• GVS

The detail I was most indecisive about was how to "present" input values to the transition procedure. Some of the alternatives I thought of were naming a single argument list to contain all of the values from all of the places; and, naming the input places and their multiplicities. Examples:

(define-transition
  (t1 args (p1 2) (p2 3) ...)
  ((p3 1) (p4 2) ...)
  ; Alternatively, use matchable
  (let ((p1-1 (car args))
        (p1-2 (cadr args))
        (p2-1 (caddr args))
        (p2-2 (cadddr args))
        ...)
    ...))

(define-transition
  (t1 (p1-args p1 2) (p2-args p2 3) ...)
  ((p3 1) (p4 2) ...)
  ; Alternatively, use matchable
  (let ((p1-1 (car p1-args))
        (p1-2 (cadr p1-args))
        (p2-1 (car p2-args))
        (p2-2 (cadr p2-args))
        ...)
    ...))

My reasoning was: what if you need a ton of tokens from a single place? Are you gonna enumerate them all? But then... there's this definition in the Statebox monograph of a k-bounded net, which is a net that never has more than k tokens in any place in any execution ever. And also the definition of a "safe net", which is a 1-bounded net. So it's a pretty big deal to have a very limitted number of tokens in a given place.

Because of that, and to get the most ergonomic bang for the typing buck, I think the syntax presented before is a good compromise.

There was also the question of representing the tokens produced. For that I quickly convinced myself that using Scheme's values is a good choice: producing several tokens needs values, producing a single token needs no extra bureaucracy. Using the language's native features is surely the way to go.

Fold Recursive Model

(Not the fold concept described in the last chapter of the Statebox monograph)

Tried modeling a fold (such as a sum), which is a recursive process, as a Petri net, basically the first on my own. Here's a rough graphic (haven't played with GraphViz settings yet):

Think of kons as add. The net must start execution with the initial value already in acc. The kons transition consumes the value from input and the value from acc, does its thing and produces the result into acc again. And peek consumes the value from acc and duplicates it into output and acc again. This transition could be a user-fired one, for example, to see the current state of the accumulator.

Alternatively it could consume the value from acc and not put it back. But that would need having a transition to produce a default value for acc. Example:

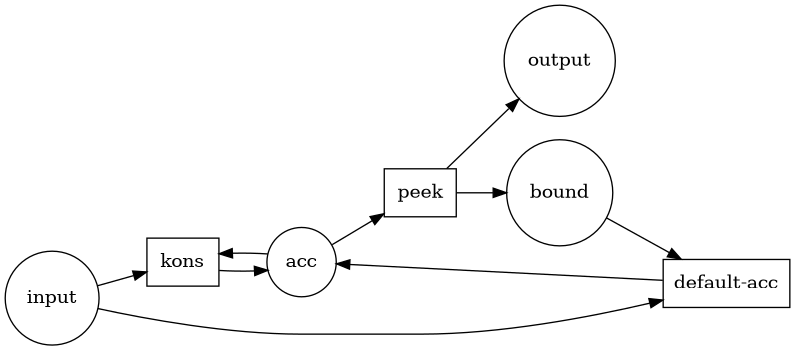
In this net acc may start empty, but bound must have a single token. When a token is produced to input, either kons or default-acc is enabled. If there's no token in acc, then there must be a token in bound, and in that case default-acc is enabled; if there's a token in ac, then there's no token in bound, and in that case kons is enabled. kons behaves as before. On the other hand, peek may consume the token from acc at any time, but does not put it back, and instead puts a dummy token in bound. This place bound is only used to "signal" that acc has no tokens, so that default-acc may move one there. default-acc simply moves an input token to acc to initialize the accumulator.

• index.html